Matemáticas : trigonometria ( parte 2 )

Ángulos notables de las razones trigonométricas

Razones trigonométricas de 30º y 60º

La altura divide al triángulo equilátero en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 60º y 30º.

Si aplicamos el teorema de Pitágoras obetenemos la altura en función del lado:

Razones trigonométricas de 45º

La diagonal divide al cuadrado en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 45º y 45º.

Si aplicamos el teorema de Pitágoras obetenemos la diagonal en función del lado:

Razones trigonométricas de ángulos notables

Circulo trigonométrico

Círculo trigonométrico. También conocido como goniométrico, es aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad. El círculo trigonométrico tiene la ventaja de ser una herramienta práctica en el manejo de los conceptos de trigonometría, pero al mismo tiempo es un apoyo teórico, pues ayuda a fundamentar y tener una idea precisa y formal de las funciones trigonométricas. Atreves del círculo trigonométrico se puede obtener de forma manual o analítica el valor aproximado de las razones trigonométricas para un ángulo determinado si se dispone de los instrumentos geométricos necesarios.

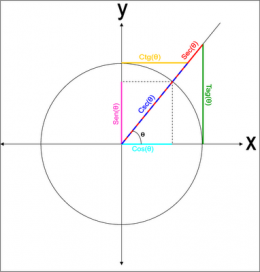
Características

Se toma como base un círculo de radio r = 1 con centro o, en el origen en el plano cartesiano. Se considera un ángulo arbitrario medido a partir del eje x positivo y en sentido positivo; o sea, en sentido contrario a las manecillas del reloj; todo ángulo puede ser colocado (y de una sola manera) de forma tal que su vértice coincida con el origen de coordenada , uno de sus lados (llamado lado inicial) coincide con la semirrecta OA y el otro lado (llamado lado terminal) quede ubicado ( a partir del inicial) en la zona de barrida en sentido contrario a la manecilla del reloj.

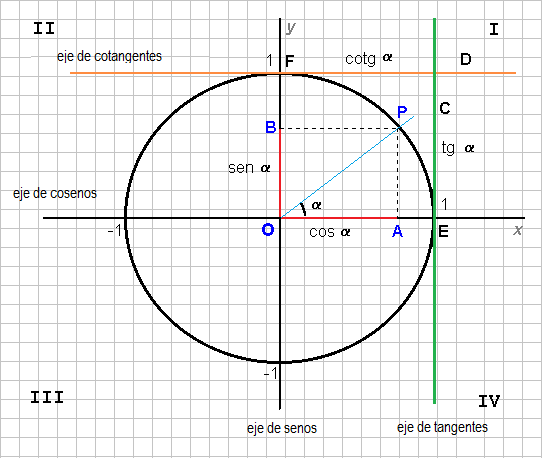
Si la semirrecta r =1 la hacemos rotar en sentido contrario a la manecilla del reloj, describe un círculo dividido en 4 cuadrantes (I, II, III, IV). Antes de que la semirrecta OP comience a rotar, coincide con el rayo OA, formando un ángulo de 0°. Cuando la semirrecta OP rota, describe un ángulo α, el cual alcanza su máximo (describiendo un círculo completo) a 360° (2π medido en radianes). De esta forma el lado terminal de cada ángulo interseca en un único punto a la [circunferencia] y podemos asociar al ángulo en ese punto de manera unívoca.

Identidades trigonométricas

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).

Notación: se define sen²α como (sen α)². Lo mismo se aplica a las demás funciones trigonométricas.