Matemáticas : Trigonometria

Trigonometría

La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'.

En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente,cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Posee numerosas aplicaciones, entre las que se encuentran: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Representación gráfica de un triángulo rectángulo en un sistema de coordenadas cartesianas.

Unidades angulares

En la medición de ángulos y, por tanto, en trigonometría, se emplean tres unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián la más utilizada, y se define como la unidad natural para medir ángulos, el grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.

· Radián: unidad angular natural en trigonometría. En una circunferencia completa hay 2π radianes (algo más de 6,28).

· Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.

· Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.

· Mil angular: unidad angular que divide la circunferencia en 6400 unidades.

Transportador en radianes

Transportador en grados sexagesimales.

Transportador en grados centesimales

Transportador en mil angular.

Las funciones trigonométricas.

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
Seno	sen
Coseno	cos
Tangente	tan
Cotangente	ctg (cot)
Secante	sec
Cosecante	csc (cosec)

Definiciones respecto de un triángulo rectángulo.

Para definir las razones trigonométricas del ángulo:

, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

· La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.

El cateto opuesto (a) es el lado opuesto al ángulo

El cateto adyacente (b) es el lado adyacente al ángulo

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo $\alpha$ , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

Funciones trigonométricas de ángulos notables

	0°	30°	45°	60°	90°
sen	0				1
cos	1				0
tan	0		1

Razones trigonométricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para

definir las razones seno, coseno y tangente, del ángulo

correspondiente al vértice A, situado en el centro de la circunferencia.

· El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.

· El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

· La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

Representación gráfica.

Representación de las funciones trigonométricas inversas en el plano cartesiano (x,y), los valores en el eje x expresados en radianes.

Ángulos y sus tipos

Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:

Tipo	Descripción
Ángulo nulo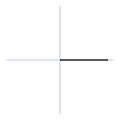	Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0°.
Ángulo agudo	Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de $\frac{\pi}{2}$ rad. Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100^g (grados centesimales).
Ángulo recto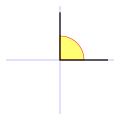	Un ángulo recto es de amplitud igual a $\frac{\pi}{2}$ rad. Es equivalente a 90° sexagesimales (o 100^g centesimales). Los dos lados de un ángulo recto son perpendiculares entre sí. La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.
Ángulo obtuso	Un ángulo obtuso es aquel cuya amplitud es mayor a $\frac{\pi}{2}$ rad y menor a $\pi\,$ rad. Mayor a 90° y menor a 180° sexagesimales (o más de 100^g y menos de 200^g centesimales).
Ángulo llano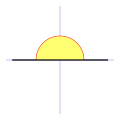	El ángulo llano tiene una amplitud de $\pi \,$ rad. Equivalente a 180° sexagesimales (o 200^g centesimales).
Ángulo oblicuo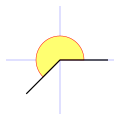	Ángulo que no es recto ni múltiplo de un ángulo recto. Los ángulos agudos y obtusos son ángulos oblicuos.
Ángulo completo o perigonal	Un ángulo completo o perigonal, tiene una amplitud de $2\pi\,$ rad. Equivalente a 360° sexagesimales (o 400^g centesimales).

Ángulos convexo y cóncavo

En un plano, dos semirrectas (no coincidentes ni alineadas) con un origen común determinan siempre dos ángulos, uno convexo (el de menor amplitud) y otro cóncavo (el de mayor amplitud):

Tipo	Descripción
Ángulo convexo o saliente	Es el que mide menos de $\pi\,$ rad. Equivale a más de 0° y menos de 180°sexagesimales (o más de 0^g y menos de 200^g centesimales).
Ángulo cóncavo, reflejo o entrante	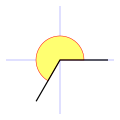Es el que mide más de $\pi\,$ rad y menos de $2 \pi\,$ rad. Esto es, más de 180° y menos de 360° sexagesimales (o más de 200^g y menos de 400^g centesimales).

Operaciones con ángulos

Suma de ángulos

Gráfica: La suma de dos ángulos es otro ángulo cuya amplitud es la suma de las amplitudes de los dos ángulos iniciales.

Numérica:

1 Para sumar ángulos se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman.

2 Si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirán a los minutos.

3 Se hace lo mismo para los minutos.

Resta de ángulos

Gráfica: La resta de dos ángulos es otro ángulo cuya amplitud es la diferencia entre la amplitud del ángulo mayor y la del ángulo menor.

Numérica:

1 Para restar ángulos se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos.

2 Se restan los segundos. Caso de que no sea posible, convertimos un minuto del minuendo en 60 segundos y se lo sumamos a los segundos del minuendo. A continuación restamos los segundos.

3 Hacemos lo mismo con los minutos.

Multiplicación de ángulos

Gráfica: La multiplicación de un número por un ángulo es otro ángulo cuya amplitud es la suma de tantos ángulos iguales al dado como indique el número.