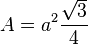Un triángulo, en geometría, es la reunión de tres segmentos que determinan tres
puntos del plano y no colineales. Cada punto dado pertenece a dos segmentos
exactamente. Los puntos comunes a
cada par de segmentos se denominan vértices del triángulo y los segmentos de recta determinados son los
lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores
del triángulo. Un triángulo es una figura estrictamente convexa.
Un triángulo tiene tres ángulos interiores, tres ángulos
exteriores, tres lados y tres vértices entre otros elementos.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para
este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico.
Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Clasificación de
los triángulos
Los triángulos se
pueden clasificar por la relación entre las longitudes de sus lados o por la
amplitud de sus ángulos.
Por las longitudes de sus lados
Por las longitudes
de sus lados, todo triángulo se clasifica:
·
Como triángulo isósceles (del
griego ἴσος "igual" y σκέλη "piernas", es decir, "con
dos piernas iguales"), si tiene dos lados de la misma longitud. Los
ángulos que se oponen a estos lados tienen la misma medida. (Tales de
Mileto, filósofo griego, demostró que un triángulo isósceles tiene
dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos;
a lados iguales, ángulos iguales ).
·
Como triángulo escaleno (del
griego σκαληνός "desigual"), si todos sus lados tienen longitudes
diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma
medida).

EQUILATERO

ISÓSCELES

ESCALENO
Por la
amplitud de sus ángulos
Por la
amplitud de sus ángulos los triángulos se clasifican en:
·
Triángulo rectángulo:
si tiene un ángulo interior recto (90°). A los
dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
·
Triángulo oblicuángulo:
cuando ninguno de sus ángulos interiores son rectos (90°). Por ello, los
triángulos obtusángulos y acutángulos son oblicuángulos.
·
Triángulo obtusángulo:
si uno de sus ángulos interiores es obtuso (mayor de 90°); los otros dos son agudos
(menores de 90°).
·
Triángulo acutángulo:
cuando sus tres ángulos interiores son menores de 90°.
 Rectángulo
Rectángulo
 Obtusángulo
Obtusángulo
 Acutángulo
Acutángulo
Clasificación según los lados y los
ángulos
Los triángulos acutángulos pueden
ser:
·
Triángulo acutángulo isósceles: con todos los
ángulos agudos, siendo dos iguales, y el otro distinto. Este triángulo es
simétrico respecto de su altura.
·
Triángulo acutángulo escaleno: con todos sus
ángulos agudos y todos diferentes, no tiene eje de simetría.
·
Triángulo acutángulo equilátero: sus tres lados y
sus tres ángulos son iguales; las tres alturas son ejes de simetría (dividen al
triángulo en dos triángulos iguales).
Los triángulos rectángulos pueden
ser:
·
Triángulo rectángulo isósceles: con un ángulo
recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro
diferente: los lados iguales son los catetos y el diferente es la hipotenusa.
Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo
recto.
·
Triángulo rectángulo escaleno: tiene un ángulo
recto, y todos sus lados y ángulos son diferentes.
Los triángulos obtusángulos pueden
ser:
·
Triángulo obtusángulo isósceles: tiene un ángulo
obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro
lado es mayor que éstos dos.
·
Triángulo obtusángulo escaleno: tiene un ángulo
obtuso y todos sus lados son diferentes.
Propiedades
de los triángulos.
Un triángulo puede ser definido como un polígono de tres
lados, o como un polígono con tres vértices.
El triángulo es el polígono más simple y el único que no tiene diagonal. Tres
puntos no alineados definen siempre un triángulo (tanto en el plano como en el
espacio).
Si se agrega un cuarto punto coplanar y no
alineado, se obtiene un cuadrilátero que
puede ser dividido en triángulos como el de la figura de la izquierda. En
cambio, si el cuarto punto agregado es no coplanar y no alineado, se obtiene un tetraedro que es
el poliedro más
simple y está conformado por 4 caras triángulares.
Todo polígono puede ser dividido en un número finito de
triángulos, esto se logra por triangulación. El número mínimo de triángulos necesarios para
esta división es n-2, donde n es el número de lados del polígono. El
estudio de los triángulos es fundamental para el estudio de otros polígonos,
por ejemplo para la demostración del Teorema de Pick.
¿Cuáles son las Rectas y los puntos notables
del triángulo?
Medianas y Baricentro
Se llama mediana a la recta que une un vértice con la mitad del lado
opuesto. En un triángulo ABC, las tres medianas se cruzan en un punto G llamado
Baricentro que es el centro de gravedad del triángulo. Cada mediana divide al
triángulo en dos triángulos de igual área. Además el Baricentro dista doble del
vértice que del punto medio del lado.
Mediatrices y Circuncentro
La mediatriz de un segmento es la recta perpendicular en su punto medio. Las mediatrices de un triángulo son las mediatrices de sus lados. El punto O donde se cortan las tres mediatrices se llama Circuncentro y equidista, es decir, está la misma distancia de los tres vértices A, B y C, es por eso que pertenece a las tres mediatrices. La circunferencia que pasa por los tres vértices se llama Circunferencia Circunscrita.
Alturas y Ortocentro
ALTURAS: se llama altura en un triángulo a la perpendicular trazada desde un vértice al lado opuesto. En un triángulo ABC, las tres alturas se cruzan en un punto llamado Ortocentro. Se puede ver que si trazamos por cada vértice una paralela al lado opuesto se obtiene otro triángulo cuyas mediatrices son justamente las alturas del triángulo primitivo.
Recta de Euler
El baricentro de un triángulo está alineado con el ortocentro y el circuncentro, y a doble distancia del primero que del segundo. La recta que contiene a estos tres puntos se llama Recta de Euler.
Bisectrices e Incentro
Se llama bisectriz a la recta que divide un ángulo en dos partes iguales. Las bisectrices de un triángulo son las bisectrices de sus ángulos. El punto I donde se cortan las tres bisectrices interiores se llama Incentro, equidista de los tres lados y por eso podemos construir una circunferencia de centro I tangente a los lados del triángulo. Dicha circunferencia se llama Circunferencia Inscrita y es la circuferencia más "grande" que se puede definir completamente contenida dentro del triángulo.

Propiedades de los triángulos
isósceles
Un triángulo es isósceles si tiene dos lados
iguales.
Propiedades
En todo triángulo isósceles:
Los ángulos opuestos a los lados iguales, son iguales.
La bisectriz del ángulo opuesto a la base, corta a la base en su punto
medio.
La bisectriz del ángulo opuesto a la base, es
perpendicular a la base.
Propiedades de los triángulos
rectángulos
Propiedades
- Todo triángulo rectángulo tiene dos ángulos agudos.
- La hipotenusa es mayor que cualquiera de los catetos.
- El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
- La suma de la hipotenusa y el diámetro de un círculo inscrito en el triángulo es igual a la suma de los catetos.
- Para efectos de área, un cateto cualquiera se puede considerar como base y el otro cateto como altura.
Propiedades de los triángulos equilatero.
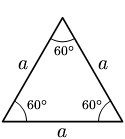
En geometría, un triángulo equilátero, es un polígono regular con
tres lados iguales. En la geometría euclídea tradicional,
los triángulos equiláteros también son equiangulares, es
decir, los tres ángulos internos también son congruentes entre sí, cada ángulo
vale 60
Propiedades
Dada
cualquier longitud a, es posible determinar por medio del Teorema de
Pitágoras las siguientes propiedades:
El
valor del área es igual a 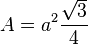
Resolución
de triangulo rectángulo
Se conocen la hipotenusa y un cateto:
Ejemplo:
Resolver el triángulo conociendo:
a = 415 m y b = 280 m.
sen B = 280/415 = 0.6747 B = arc sen 0.6747 = 42° 25′
C = 90° - 42° 25′ = 47° 35′
c = a cos B c = 415 · 0.7381 = 306. 31 m
Se conocen los dos catetos:
Problema de Resolución de triangulo rectángulo
Para medir la altura de una torre nos situamos en un punto del suelo y vemos el punto más alto de la torre bajo
un ángulo de 60o. Nos acercamos 5 metros a la torre en línea recta y el ángulo es de 80o. Halla la altura de la
torre.
Referencias.
http://es.wikipedia.org/wiki/Tri%C3%A1ngulo
http://geogebra.geometriadinamica.org/ventana_rectas_notables.html
http://www.vitutor.com/al/trigo/tri_12.html
http://186.65.85.243/naval/webesnm/apoyo/ejerciciosresoluciondetriangulosrectangulos.pdf
https://sites.google.com/a/roberprof.com/euclides/Home/triangulos/propiedades-de-los-triangulos-isosceles
http://es.wikipedia.org/wiki/Tri%C3%A1ngulo_rect%C3%A1ngulo
http://es.wikipedia.org/wiki/Tri%C3%A1ngulo_equil%C3%A1tero